 |
從此數學家們除了希望用傳統方法證明以外,也開始向著機械程式的驗證著眼,用以窮盡所有的可能性。1913年,美國數學家伯克霍夫(George David Birkhoff)利用肯普的想法和自己的新技巧,發展了一套能夠證明大某些大的構形的可約性的方法。而數學家希什(Heinrich Heesch)宣稱可用尋找可約構形的不可避免組來證明四色猜想。在1950年,希什估計這樣的圖約有一萬個,但在當時要檢查所有這些圖似是不可能。
隨著電腦技述的進步,以及希什的努力,他利用伯克霍夫所發展的原理,編訂了程序準備攻克這個猜想。希什引進了一個「放電」(discharging)的概念來輔助證明,但仍然面對一定的困難,因為要計算的數量可能很大。1970年數學家黑肯(Wolfgang Haken)作出如下的判斷:肯定不會對四色猜想給出一個非機器證。但在沒有更為强有力的計算機之前能否用計算機給出證明也存有懷疑。
1972年,黑肯和阿佩爾(Kenneth Appel)設計了一份計算程序,它能作出特殊類型的「放電」過程,還能給出從最重要的情況得出的構形作為輸出。經過不斷的研究改進及修改,最後找到一個可行的程序,但實際執行這個程序將會複雜到甚麼程度,還是一個疑問。在1976年1月6日,他們確定了一些細節,設計了適當的程序,利用三部電腦,運行了1200多個小時,其「放電」過程大約包括500個特殊「放電」情況,需要用人工分析約10000個頂點帶電的鄰域,最後找出2000多個構形需要用機器分析其可約性。由這些圖便能證明這個「四色猜想」,將之變為「四色定理」,解決了這個困擾許多數學家一百多年的難題。
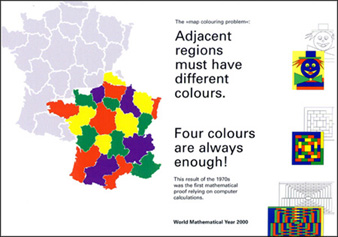 |
這個「四色定理」也是首個倚靠機器來證明的重要數學定理,因此很難由其他數學家直接檢證,所以初時數學家也對此有所懷疑。雖然如此,但在1977年的兩篇有關的論文卻已能說服所有人這個四色定理的真確性。
| 上一章 | 第一章 |
| 參考書目: | |
| 1. | 徐本順、解恩澤編著,《數學猜想集》,湖南科學技術出版社,湖南,1999。 |
| 2. | 李學數著,《數學和數學家的故事 第一集》,九章出版社,台灣,1993。 |